Особенности шестиугольной призмы и как рассчитать объем

семиугольная призма это геометрическая фигура, которая, как следует из названия, включает в себя два геометрических определения: призма и семиугольник.

«Призма» - это геометрическая фигура, ограниченная двумя равными и параллельными основаниями, а их боковые грани являются параллелограммами..

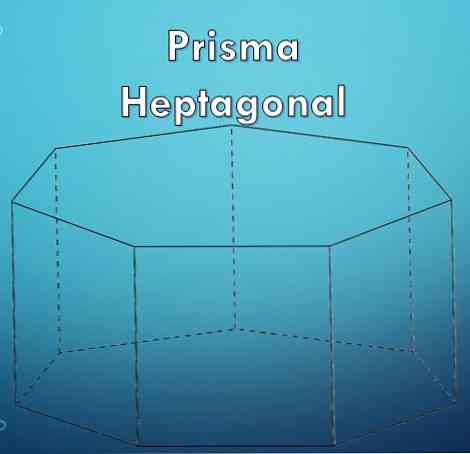
«Семиугольник» - это многоугольник, образованный семью (7) сторонами. Так как семиугольник является многоугольником, может быть, что он правильный или неправильный.

Полигон называется правильным, если все его стороны имеют одинаковую длину и их внутренние углы имеют одинаковую длину, их также называют равносторонними многоугольниками; в противном случае говорят, что многоугольник неправильный.

Характеристики семиугольной призмы

Ниже приведены некоторые особенности, которые имеют семиугольную призму, такие как: его конструкция, свойства его оснований, площадь всех его граней и его объем.

1- Строительство

Для построения семиугольной призмы необходимы два семиугольника, которые будут являться ее основаниями и семь параллелограммов, по одному с каждой стороны семиугольника..

Начните с рисования семиугольника, затем нарисуйте семь вертикальных линий равной длины, которые исходят из каждой его вершины..

Наконец, другой семиугольник нарисован так, что его вершины совпадают с концом линий, нарисованных на предыдущем шаге..

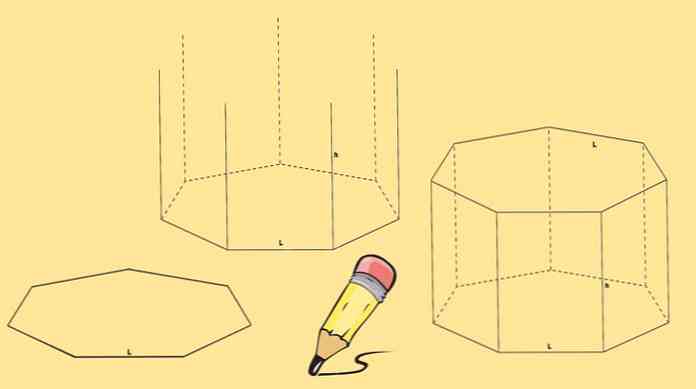
Нарисованная выше семиугольная призма называется прямой семиугольной. Но вы также можете иметь наклонную семиугольную призму, как показано на следующем рисунке..

2- Свойства его оснований

Поскольку их основания являются семиугольниками, они согласуются с тем, что диагональное число равно D = nx (n-3) / 2, где «n» - число сторон многоугольника; в этом случае имеем D = 7 × 4/2 = 14.

Также видно, что сумма внутренних углов любого семиугольника (правильного или неправильного) равна 900º. Это можно проверить по следующему изображению.

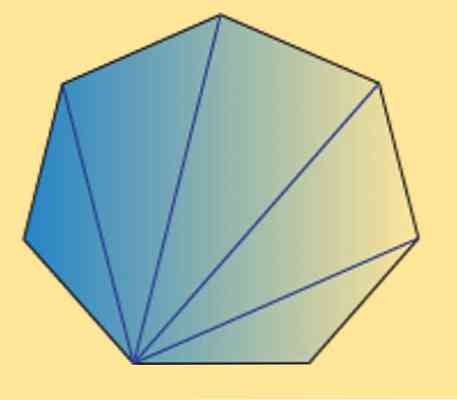
Как видите, существует 5 внутренних треугольников, и, используя сумму внутренних углов треугольника, равную 180º, можно получить, что желаемый результат.

3- Площадь, необходимая для построения семиугольной призмы

Поскольку его основания - два семиугольника, а его стороны - семь параллелограммов, площадь, необходимая для построения семиугольной призмы, равна 2xH + 7xP, где «H» - площадь каждого семиугольника, а «P» - площадь каждого параллелограмма..

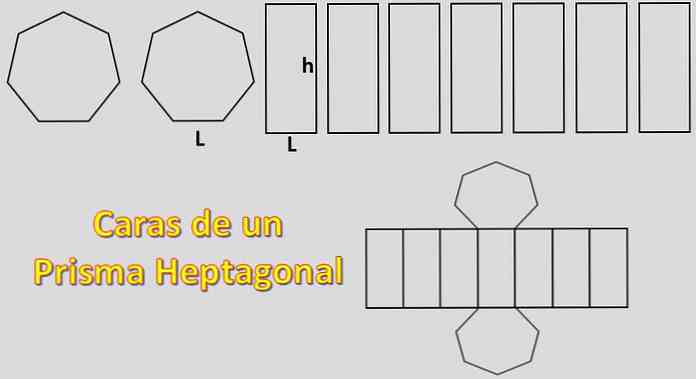
В этом случае площадь правильного семиугольника будет рассчитана. Для этого важно знать определение апотемы.

Апофем - это перпендикулярная линия, идущая от центра правильного многоугольника к средней точке любой из его сторон..

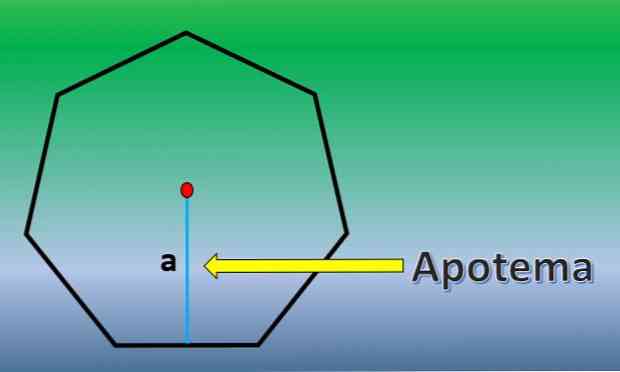
Как только апофем известен, площадь семиугольника H = 7xLxa / 2, где «L» - длина каждой стороны, а «a» - длина апофема..

Площадь параллелограмма легко вычисляется, определяется как P = Lxh, где «L» - это та же длина стороны семиугольника, а «h» - высота призмы..

В заключение, количество материала, необходимого для построения семиугольной призмы (с правильными основаниями), составляет 7xLxa + 7xLxh, то есть 7xL (a + h).

4- Том

Как только площадь основания и высота призмы известны, объем определяется как (базовая область) x (высота).

В случае семиугольной призмы (с регулярным основанием) ее объем равен V = 7xLxaxh / 2; также может быть записано как V = Pxaxh / 2, где «P» является периметром правильного семиугольника.

ссылки

1. Биллштейн Р., Либескинд С. и Лотт Дж. У. (2013). Математика: проблемный подход для учителей базового образования. Лопес Матеос Эдиторес.
2. Fregoso, R.S. & Carrera, S.A. (2005). Математика 3. Редакция Прогресо.
3. Галлардо Г. & Пилар П. М. (2005). Математика 6. Редакция Прогресо.
4. Гутьеррес, С. Т. и Сиснерос, М. П. (2005). 3-й курс математики. Редакция Прогресо.
5. Кинси Л. и Мур Т. Э. (2006). Симметрия, форма и пространство: введение в математику через геометрию (иллюстрированный, перепечатанный ред.). Springer Science & Business Media.
6. Митчелл, C. (1999). Ослепительный дизайн Math Line (Иллюстрированный ред.). Scholastic Inc.
7. Р., М. П. (2005). Я рисую 6º. Редакция Прогресо.