Сколько краев у гексагональной призмы?
Знать сколько ребер имеет шестиугольная призма значение «край», «призма» и «шестиугольник» должны быть известны. Первые два понятия являются общими определениями, а третье понятие связано с формой геометрической фигуры..
Когда речь идет о шестиугольнике, упоминается шестиугольник (многоугольник). Приставка «гекса» указывает на то, что многоугольник имеет шесть сторон.

Ребро - это ребро объекта. Геометрически это линия, соединяющая две последовательные вершины геометрической фигуры.
Призма - это геометрическая фигура, ограниченная двумя параллельными и равными основаниями, а их боковые грани являются параллелограммами..
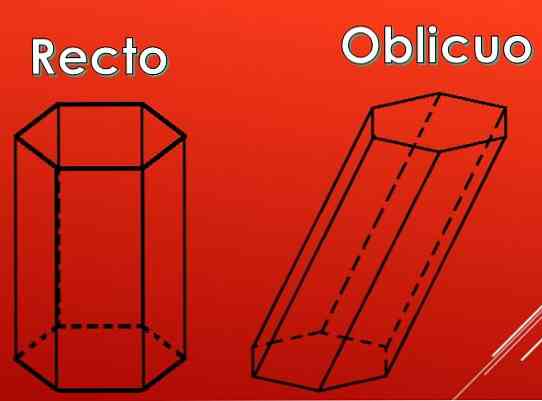
На следующем изображении видно, что боковые грани шестиугольной призмы могут быть прямоугольниками, но они также могут быть параллелограммами..
По типу параллелограммов премии могут быть классифицированы на два типа: прямые и косые.
Как посчитать края шестиугольной призмы?
Число ребер, которые будет иметь шестиугольная призма, не изменится, если это прямая или наклонная призма. Кроме того, количество ребер также не зависит от длины сторон.
Подсчет граней шестиугольной призмы можно выполнить несколькими способами. Вот два способа:
1- Разложить призму
Один из способов подсчета ребер состоит в разложении шестиугольной призмы на двух ее основаниях и боковых гранях. Таким образом, вы получите два шестиугольника и параллелограмм с пятью внутренними линиями.
Каждый шестиугольник имеет шесть ребер, поэтому призма будет иметь более 12 ребер.
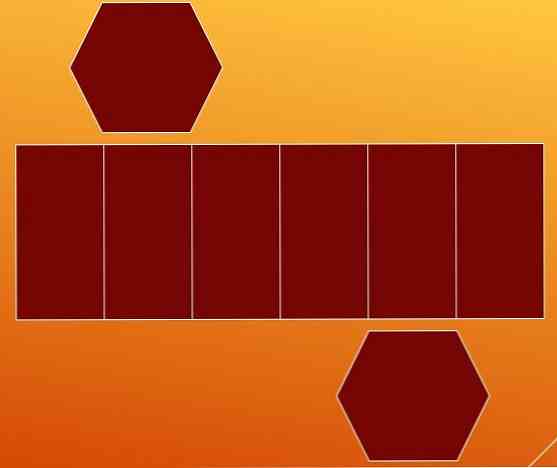
На первый взгляд считается, что параллелограмм содержит девять ребер (семь вертикальных и два горизонтальных). Но удобно остановиться, чтобы проанализировать этот случай.
Когда параллелограмм согнут для образования призмы, видно, что первая строка слева соединится с последней строкой справа, с которой обе линии представляют одно ребро.
Но как насчет двух горизонтальных линий?
Когда все части снова собраны вместе, горизонтальные линии будут соединены, каждая, с шестью краями каждого шестиугольника. По этой причине считать их отдельно было бы ошибкой.
Таким образом, параллелограмм содержит шесть ребер призмы, которые вместе с 12 ребрами, подсчитанными в начале, дают в общей сложности 18 ребер.
2.- Проектирование каждого края
Другой способ, намного проще сосчитать ребра, это использование факта, что основания шестиугольных призм являются шестиугольниками, тогда каждое основание имеет шесть ребер.
С другой стороны, из каждой вершины шестиугольника одно ребро проецируется на соответствующую вершину другого шестиугольника; то есть есть шесть ребер, которые соединяют одну базу с другой.
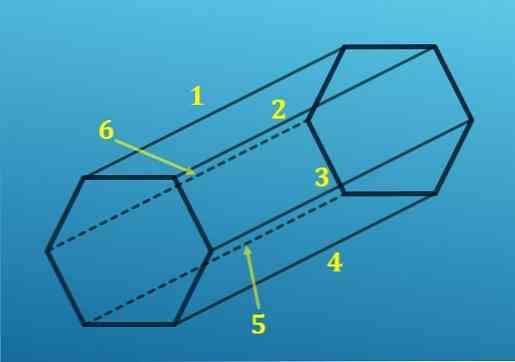
Добавив все ребра, вы получите в общей сложности 18 ребер.
заключение
Можно показать, что число ребер призмы в три раза больше количества ребер, которые имеет многоугольник, который образует ее.
Следовательно, пятиугольная призма будет иметь 3 * 5 = 15 ребер, семиугольная призма будет иметь 3 * 7 = 21 ребро, и, таким образом, она может быть применена к любой призме..
ссылки
- Биллштейн Р., Либескинд С. и Лотт Дж. У. (2013). Математика: проблемный подход для учителей базового образования. Лопес Матеос Эдиторес.
- Fregoso, R.S. & Carrera, S.A. (2005). Математика 3. Редакция Прогресо.
- Галлардо Г. & Пилар П. М. (2005). Математика 6. Редакция Прогресо.
- Гутьеррес, С. Т. и Сиснерос, М. П. (2005). 3-й курс математики. Редакция Прогресо.
- Кинси Л. и Мур Т. Э. (2006). Симметрия, форма и пространство: введение в математику через геометрию (иллюстрированный, перепечатанный ред.). Springer Science & Business Media.
- Митчелл, C. (1999). Ослепительный дизайн Math Line (Иллюстрированный ред.). Scholastic Inc.
- Р., М. П. (2005). Я рисую 6º. Редакция Прогресо.


