Коллинеарная система и примеры
коллинеарные векторы Они являются одним из трех типов существующих векторов. Речь идет о тех векторах, которые находятся в одном направлении или направлении действия. Это означает следующее: два или более векторов будут коллинеарными, если они расположены в виде прямых линий, параллельных друг другу.
Вектор определяется как величина, применяемая к телу, и характеризуется как имеющий направление, смысл и масштаб. Векторы могут быть найдены в плоскости или в пространстве и могут быть разных типов: коллинеарные векторы, параллельные векторы и параллельные векторы.

индекс
- 1 колинеальный вектор
- 2 Характеристики
- 2.1 Пример 1
- 2.2 Пример 2
- 2.3 Пример 1
- 3 Коллинеарная векторная система
- 3.1 Коллинеарные векторы с противоположными значениями
- 3.2 Коллинеарные векторы с одинаковым смыслом
- 3.3 Коллинеарные векторы с равными величинами и противоположными значениями
- 4 Разница между коллинеарными и параллельными векторами
- 5 ссылок
Коллинеарные векторы
Векторы коллинеарны, если линия действия одного является точно такой же линией действия всех других векторов, независимо от размера и смысла каждого из векторов..
Векторы используются в качестве представлений в различных областях, таких как математика, физика, алгебра, а также в геометрии, где векторы коллинеарны только тогда, когда их направление одинаково, независимо от того, имеет ли их значение значение.
черты
- Два или более вектора коллинеарны, если соотношение между координатами равно.
Пример 1
У нас есть векторы m = m_x; m_y и n = n_x; n_y. Они коллинеарны, если:
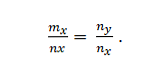
Пример 2
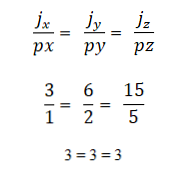
- Два или более векторов коллинеарны, если произведение или вектор умножения равен нулю (0). Это связано с тем, что в системе координат каждый вектор характеризуется своими соответствующими координатами, и если они пропорциональны друг другу, векторы будут коллинеарными. Это выражается следующим образом:
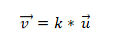
Пример 1
У нас есть векторы a = (10, 5) и b = (6, 3). Чтобы определить, являются ли они коллинеарными, применяется теория детерминантов, которая устанавливает равенство перекрестных произведений. Таким образом, вы должны:
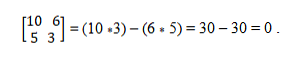
Коллинеарная векторная система
Коллинеарные векторы представлены графически с использованием направления и смысла их, учитывая, что они должны проходить через точку приложения и модуль, который имеет определенный масштаб или длину.
Система коллинеарных векторов формируется, когда два или более векторов воздействуют на объект или тело, представляя силу и действуя в одном направлении..
Например, если к телу приложены две коллинеарные силы, их результат будет зависеть только от направления, в котором они действуют. Есть три случая, которые:
Коллинеарные векторы с противоположными чувствами
Результирующий из двух коллинеарных векторов равен сумме этих:
R = Σ F = F1 + F2.
пример
Если на тележку F действуют две силы1 = 40 Н и F2 = 20 Н в обратном направлении (как показано на рисунке), результат:
R = Σ F = (- 40 Н) + 20 Н.
R = - 20 Н.
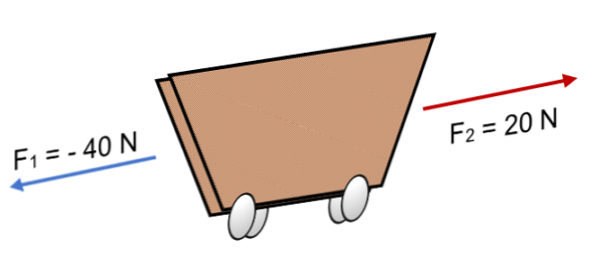
Коллинеарные векторы с одинаковым смыслом
Величина результирующей силы будет равна сумме коллинеарных векторов:
R = Σ F = F1 + F2.
пример
Если на тележку F действуют две силы1 = 35 Н и F2 = 55 Н в том же направлении (как показано на рисунке), результат:
R = Σ F = 35 Н + 55 Н.
R = 90 Н.
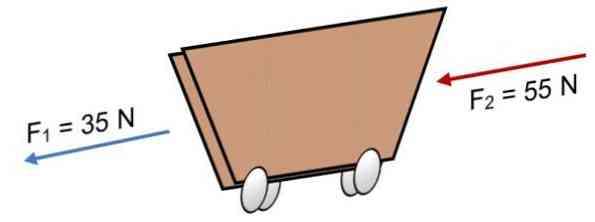
Положительный результат показывает, что коллинеарные векторы действуют влево.
Коллинеарные векторы с одинаковыми величинами и противоположными значениями
Результирующий из двух коллинеарных векторов будет равен сумме коллинеарных векторов:
R = Σ F = F1 + F2.
Поскольку силы имеют одинаковую величину, но в противоположном направлении, то есть одно будет положительным, а другое отрицательным, при сложении двух сил результирующее значение будет равно нулю.
пример
Если на тележку F действуют две силы1 = -7 N и F2 = 7 Н, которые имеют ту же величину, но в противоположном направлении (как показано на рисунке), результат:
R = Σ F = (-7 Н) + 7Н.
R = 0.
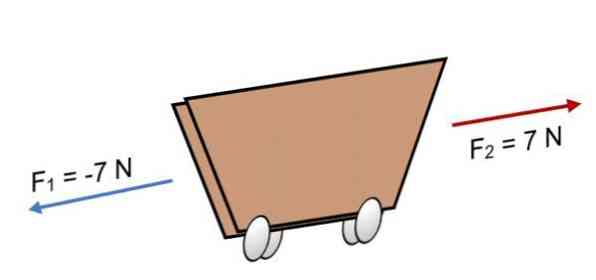
Поскольку результат равен 0, это означает, что векторы сбалансированы друг с другом и, следовательно, тело находится в равновесии или в состоянии покоя (оно не будет двигаться).
Разница между коллинеарным и параллельным векторами
Коллинеарные векторы характеризуются наличием одинакового направления на одной линии или потому, что они параллельны линии; то есть они являются векторами прямых параллельных линий.
С другой стороны, параллельные векторы определены, потому что они находятся в разных направлениях действия, которые перехвачены в одной точке.
Другими словами, они имеют одну и ту же точку отправления или прибытия - независимо от их модуля, направления или направления - образуя угол между ними.
Системы параллельных векторов решаются математическими методами или графами, которые являются методом параллелограмма сил и методом многоугольника сил. По ним будет определяться значение результирующего вектора, который указывает направление, в котором будет двигаться тело..
По сути, основное различие между коллинеарными векторами и параллельными векторами заключается в линии действия, в которой они действуют: коллинеарные действуют в одной линии, тогда как параллельные в разных.
То есть коллинеарные векторы действуют в одной плоскости: «X» или «Y»; и одновременный акт в обеих плоскостях, начиная с одной и той же точки.
Коллинеарные векторы не находятся в одной точке, как параллельные, потому что они параллельны друг другу.
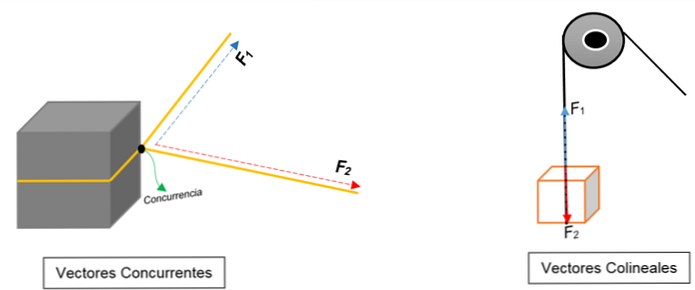
На левом изображении вы можете увидеть блок. Он связан веревкой, а узел делит его на две части; когда тянуть в разные стороны и с разными силами, блок будет двигаться в том же направлении.
Представлены два вектора, которые совпадают в точке (блоке), независимо от их модуля, смысла или направления.
Вместо этого на правом изображении появляется шкив, который поднимает коробку. Веревка представляет собой линию действий; когда его тянут, на него действуют две силы (векторы): одна сила натяжения (при подъеме на блок) и другая сила, та, которая воздействует на вес блока. Оба имеют одинаковое направление, но в противоположных направлениях; не соглашайтесь в точке.
ссылки
- Estalella, J. J. (1988). Векторный анализ. Том 1.
- Гупта А. (с.ф.). Тата МакГроу-Хилл Образование.
- Jin Ho Kwak, S.H. (2015). Линейная алгебра. Springer Science & Business Media.
- Montiel, H.P. (2000). Физика 1 для технологического бакалавриата. Патрия Редакционная группа.
- Сантьяго Бурбано де Эрсилья, C.G. (2003). Общая физика Редакция Тебар.
- Синха, К. (с.ф.). Учебник математики XII том 2. Публикации Растоги.


